- 上一篇:Gd掺杂对Ca3Co4O9热电材料的自旋熵影响研究
- 下一篇:利用铁尾矿制备烧结砖的研究
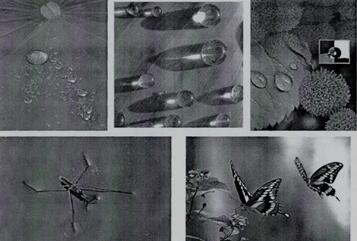
图1-1 自然界中的超疏水现象
固体的一个非常重要的性质是固体表面对于液体的润湿性。在以下方面发挥着非常重要地作用:工业、农业以及日常生活中 [4]。例如,植物根部吸收水分,出现在眼镜上的水雾和建筑物外墙的水渍等,与它们表面润湿性能都有关。润湿性能应用十分广泛:微电子、印刷、造纸、交通乃至新材料的制备合成,以及医药、生物芯片等,都与润湿能力有十分密切的关系。在科学研究角度考虑,对润湿问题研究既有重要的理论意义,也有重大实际应用的价值。论文网
对固体表面来说,当液滴接触时,液滴会保持部分的形状,或者,铺展开来,形成一层液膜。通过测量接触角可以描述这一性质。超亲水表面是当水滴在固体表面上的接触角接近0°时的固体表面;超疏水表面是当水滴所形成的接触角大于150°时的固体表面。
固体表面的润湿性的极端特例,在防水、自净、减阻降噪音和光电材料等方面,超疏水性/超疏水材料有十分广阔的应用前景。因此,近20年来,其吸引了大量材料科学研究者的关注和兴趣,在最近的几年更是倍受瞩目。
1.2 超疏水表面的基本理论
1.2.1 静态接触角
一液滴滴在固体表面上,如图1-2。设在固、液、气的相界面上,固气界面张力是γsg,固液界面张力是γsl,气液表面张力是γlg。三相交界处的自固液界面经过液体内部到气液界面的夹角叫做接触角,用θ表示。那么,三相界面的张力γsg、γsl、γlg一般满足Young´s方程[5]:
cosθ = (γsg - γsl)/γlg (1-1)
图1-2 接触角的定义
但是Young´s方程只适用在理想的固体表面。对具有一定的粗糙度的实际固体的表面来说,表面的润湿性是由表面的化学组成和其粗糙度两者一起决定的。通过降低固体表面能,这样能够提高其疏水性。但要想获得更加疏水的表面,就要考虑表面的粗糙度对表观接触角的影响。
Wenzel和Cassie分别对于表面的粗糙结构对接触角影响进行了大量深入研究,并且建立数学模型,即Wenzel模型和Cassie模型。
1.2.2 Wenzel模型
任何固体的表面都不会绝对光滑,对实际固体的表面,表面的粗糙度对润湿的能力的影响需要考察,Wenzel已经意识到这一点[6],他认为,当液滴与固体的表面接触,液体会完全充满粗糙的表面上的小缝隙(Wenzel模型),只为固液的接触。如图1-3A所示。Wenzel对于Young’s方程,做了下面的修改:
cosθW = r (γsg - γsl) /γlg=rcosθ (1-2)
在方程中,r定义是粗糙度常数,是一个无量纲常数,表示固体真实的表面积和理想的表面积的比。θW为粗糙的表面平衡接触角。方程(1-2)说明了如下两点:(1)当θ<90°,θW随粗糙度变大而减小,变成更加亲水;(2)当θ>90°,θW随粗糙度变大而变大,变成更加疏水。
图1-3 A水滴在粗糙固体表面的Wenzel模式;B水滴在粗糙固体表面的Cassie模式。
1.2.3 Cassie模型