Fluent数值研究热毛细力驱动的方腔流输运机理(2)

菜单

3.5物理条件及边界条件 16

3.6本章小结… 16

4结果分析…17

4.1不同条件下的自然对流 17

4.2微重力条件下的自然对流和热毛细对流…21

4.3 不同宽深比下热毛细对流23

4.4 本章小结 32

结论 … 33

致谢 … 34

参考文献35

附录A UDF编程边界条件 37

1 绪论

1.1 本课题的背景

自然界中的对流是非常常见的一种现象，普遍存在的一种流体运动方式，它与流体内部热物理有着密切的关系，对于热对流的研究有着深远且有影响的历史。随着科技的进步，人们对航天领域的探索和空间技术的发展，人们对微重力科学领域的探索不断迈向新高度，由于重力作用的消失而一些物理运动过程便充分显露出来，使得以前在重力场中难以发现的一些现象被人们逐渐重视起来。如表面张力，它是不随重力的消失而消失的。

热毛细对流，是一种由于自由面表面张力的变化引起的剪切力，即热毛细力而驱动的一种对流现象。它不仅存在于地球重力场中，也依然存在于微重力环境下，不会因重力场的消失而消失，它常常存在于特征尺寸较小的体系中或微重力条件下。现如今热毛细对流受到人们越来越多的重视，在前人已证实的大量实验中，证明了热毛细对流对于微重力条件下的物质输运过程有着明显的影响，并且在航空航天领域、晶体生长、薄膜科学、沸腾与凝结换热等方面有着显著的影响。

近年来，人们越来越多的发现热毛细对流对于物理过程有着深远的影响，如晶体生长往往由于热毛细对流而产生波动条纹等杂志现象的出现，所发展的浮区技术便是一种在微重力条件下来实现更高质量的半导体晶体的很有前途的容积方法。

1.2 概述

1.2.1自然对流及热毛细对流

在重力场作用下，流体由于温度或浓度的不均匀会造成密度的不均匀，使得密度低的流体朝着与重力场相反的方向移动，即受到浮力的作用，当其足以克服流体粘性阻力的作用时，流体液层中就会产生对流，称之为自然对流。自然对流是人们熟悉的一种流体形式，它与人类生活、生产和自然现象广泛相连。人们最熟悉的自然对流形式便是Rayleigh-Benard对流，即当存在温度梯度且与重力方向平行时，产生的浮力作用克服重力，进而驱动流体形成对流趋势[1]。经典的Rayleigh-Benard自然对流如图1.1所示，其中上壁面为恒温坚壁，温度为T0，下壁面也为恒温坚壁，但是维持一个较上壁面高的温度T0+ T，温差 T引起流体中的密度变化，产生与重力方向相反的浮生力，进一步产生自然对流。

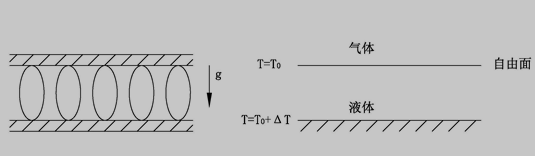
Rayleigh-Benard 自然对流体系

(a)经典的Rayleigh-Benard自然对流（b）自由面液层Rayleigh-Benard自然对流

图1.1 Rayleigh-Benard 自然对流体系

热毛细对流又称Marangoni对流[2]，是由于流体表面张力不均匀，产生表面张力梯度即热毛细力，由它驱动的一种流动形式。在地面条件下，一般情况下Marangoni对流非常微弱，几乎不对流体流动产生影响，只存在于特征尺寸很小的体系中，而且往往与重力的作用耦合在一起。

在地球表面重力场中热毛细对流往往被浮力驱动的对流所掩盖。在微重力环境下，重力作用的消失在很大程度上抑制了浮力对流的发生，此时，与重力作用无关的由表面张力梯度驱动的流动就突出起来。随着引力的消失，自然对流继而消失，而表面张力不会随着重力的消失而消失，所以其引起的热毛细对流则依然存在，并起着特别重要的作用。热毛细对流作为更广泛的一类流动正成为微重力科学中人们必须重视的一类典型问题。