- 上一篇:各向同性介质填充场域时矢量有限元法系数矩阵的推导
- 下一篇:基于SUSAN角点检测算法研究与实现
1.1.2 图像融合的研究意义
小波分析应用的领域十分广泛,它包括:数学领域;信号分析、图像处理;量子力学、理论物理;计算机分类与识别;音乐与语言的人工合成;医学成像与诊断;地震勘探数据处理;大型机械的故障诊断等方面;例如,在数学方面,它已用于分析数值、快速数值方法的构造、控制论、构造曲线曲面、求解微分方程等。在信号分析方面的滤波、传递、降噪声、压缩等。在图像处理方面的图像压缩、去污、分类、识别与诊断等。在医学成像方面的降低B超、核磁共振成像的时间、CT,提高分辨率等。
(1)小波分析主要应用于图像融合和信号方面。它具有较高的融合准确度,良好的融合效果,稳定可靠的信号与图像的总数据还有能准确的传递信息的特点。小波分析有各式各样的融合方法,比较突出常用的是基于多分辨分析的图像融合和应用Mallat小波变换算法进行图像数据融合等。
(2)小波在信号分析中也是重要的构成。类如提取分离微弱信号方面、检测多角度边缘方面、分析时域等
(3)在工程技术等方面的应用。类如计算机视觉、湍流、曲线设计、远程宇宙的研究、微机图形学与生物医学方面等[4]。
MATLAB是高性能的工程以及科学计算软件,还能对计算数据进行可靠具体的分析以及整理,而且还有设计程序和可视化图形表现的功能。因此,MATLAB的适用的领域非常的宽阔,前景十分美好。它除了应用在数学计算和分析外,还在自动控制、系统仿真、图形图像分析、数字信号领域、数理统计、人工智能、通信工程、虚拟现实技术、金融系统等领域都发挥着重要的作用[4]。目前小波分析广泛的应用在各种工程领域,深受科学工作者的喜爱。MATLAB在原有的功能外又逐渐增加了各个领域专家的成果,工具箱越来越繁多,到现在已经包含信号处理、图像处理、系统辨识、通信、小波分析、优化以及控制系统等不同应用领域的工具箱。因此,此课题的研讨是非常有意义的,后面的实验仿真也需要此软件的辅助[3]。
1.2 主要内容
本文提供了一种多聚焦的图像融合方法,把原始图像通过小波分解到不同的频域来解析高频系数和低频系数的选择原则。在很多情况下,单一的图像信息不能够完整科学的解析检测目标或场景,因为会受到目标的状态,位置,还有其他的一些影响。图像融合是将多幅图像融合在一起,变成一幅合成图像,它可以准确可靠的表示研究对象的细节特征,在很多领域,图像融合具有很大的应用,有许多实际性的意义。
2. 小波变换理论基础
2.1 小波变换
小波分析是一门蓬勃发展的创新学科,它以现代调和分析为基础,其基础理论知识涉及广泛,同时具有理论指导和实践应用的广泛双重意义。本文仅对多聚焦图像融合整体思想进行讨论。
2.1.1小波变换的思想 来!自~751论-文|网www.751com.cn
小波变换不仅延续了Gabor的加窗傅立叶变化的一些思想,而且克服了傅立叶变换窗口大小不能随频率变化的缺点,其基本思想来于可变窗口的伸缩和平移。小波变换可以通过伸缩和平移得到了一个小波基函数。在特定条件下每一个有限信号都可以时-频分解,以适应不同分辨率的需求[5]。
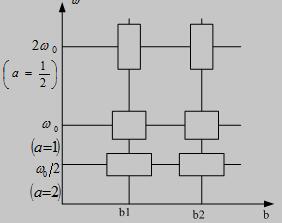
图2-1 时-域平面划分
在加窗傅立叶中,窗函数变换在时频相平面中窗口的大小是不随时频变化的。即其分辨率不改变,如图2-1所示,窗函数在时频相平面中随中心频率改变而改变,频窗在低频处会变窄,在高频变宽,所以它特别擅长分析不平稳信号。传统的信号分析是由傅里叶变换为基础,然而傅立叶分析是整体的变换,它只提供信号的频域信息,因此不能体现信号的时频局域性质,此性质与非平稳信号吻合[5]。