- 上一篇:制导火箭导引规律研究
- 下一篇:ANSYS某次口径弹丸支撑装置设计
a) 制导火箭弹数学模型的建立:为描述制导火箭弹的运动过程,需定义几个常用坐标系并给出坐标系转换方程,然后建立制导火箭弹三自由度质点弹道模型,弹体的俯仰、偏航运动方程组和锥形运动方程组,根据方程组分析运动特性。
b) 制导律和理想速度曲线设计:根据末段的飞行任务需求,选取适当的控制理论进行制导律设计,并进行计算机仿真,根据影响规律选出适当的控制参数,由终端约束条件反推出理想速度曲线。进行中末制导交接班条件优化设计。
c) 锥形运动参数的设计:根据锥形运动方程组分析影响制导火箭弹速度的参数,并针对各参数进行计算机仿真,分析锥形运动参数对制导火箭弹速度的影响规律,设计出合理的锥形运动参数。
d) 仿真验证:根据所设计的制导律参数和锥形运动参数进行仿真,验证减速效果。
2 制导火箭弹数学模型
为了正确描述制导火箭弹的空间运动,研究运动特性,需定义一些常用坐标系,建立空间运动方程。由于选取的坐标系的不同,所建立的运动方程的形式和复杂程度就会有所不同,这将对求解运动方程的难易和运动参数直观程度产生影响。本章将定义一些常用坐标系,对制导火箭弹进行受力分析,建立弹箭的数学模型,并对弹道方案进行设计,通过仿真初步分析其弹道特性。
2.1 坐标系定义及坐标系转换
2.1.1 坐标系定义
a) 地面坐标系Axyz
地面坐标系是与地球表面固连的,坐标系原点A位于发射点;Ax轴为弹道平面与水平面的交线,以指向目标的方向为正;Ay轴沿铅垂线向上,Az轴与另外两轴垂直并构成右手直角坐标系。
b) 弹体坐标系Ox1y1z1
弹体坐标系的原点O位于质心;Ox1轴与弹体的纵轴重合,以指向头部的方向为正;Oy1轴位于弹体的纵向对称平面内并与Ox1轴垂直,以指向上的方向为正;Oz1轴垂直于另外两轴,并构成右手直角坐标系。
c) 弹道坐标系Ox2y2z2
弹道坐标系原点O位于弹体的瞬时质心;Ox2轴与速度矢量 的方向重合;Oy2轴位于包含速度矢量 的铅垂平面内并垂直于Ox2轴,以指向上的方向为正;Oz2轴垂直于另外两轴并构成右手直角坐标系。
d) 速度坐标系Ox3y3z3
速度坐标系原点O位于弹体的质心;Ox3轴与速度矢量 的方向重合;Oy3轴位于弹体的纵向对称平面内并与Ox3轴互相垂直,以指向上的方向为正;Oz3轴垂直于另外两轴并构成右手直角坐标系。
2.1.2 坐标系转换
制导火箭弹在飞行过程中受到重力、空气动力、发动机推力,但这些力分别定义在不同的坐标系中,在建立火箭弹运动标量方程时,必须将各量向同一坐标轴投影,因此要进行坐标系转换。
a) 地面坐标系(Axyz)与弹体坐标系(Ox1y1z1)之间的转换
弹体坐标系相对地面坐标系的姿态通常用三个角度来确定,如图2.1所示,分别定义如下:
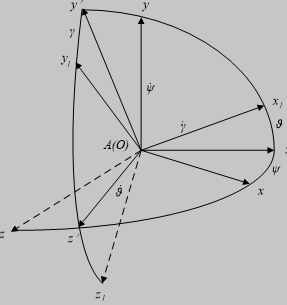
图2.1 地面坐标系与弹体坐标系之间的关系
俯仰角 :弹体的纵轴(Ox1轴)与水平面(Axz平面)之间的夹角。当弹体纵轴指向水平面上方, 角为正,反之为负。
偏航角 :弹体纵轴在水平面内投影(即图中Ax′)与地面坐标系Ax轴之间的夹角。迎 Ay 轴俯视观察,若由 Ax 轴转至 Ax′轴是逆时针旋转,则ψ角为正,反之为负。
倾斜角 :弹体坐标系的 Oy1轴与包含弹体纵轴的铅垂平面(即图中Ax′y′)之间的夹角。由弹体尾部顺纵轴前视,若 Oy1轴位于铅垂面 Ax′y′的右侧(即弹体向右倾斜),则 角为正,反之为负。