- 上一篇:雷达目标模拟器的研究现状与发展
- 下一篇:货币识别器研究现状和发展趋势
高次谐波在实验上首次被观测是在上世纪80年代,实验得到的谐波谱呈现出了特有的谐波平台[10,11]。到了90年代,大多数实验工作都集中于扩展谐波平台,即产生更高频率和更短波长的谐波,从~20 nm到~7 nm。而目前在实验上,高次谐波辐射已经能够进入“水窗”阶段[5]。高次谐波实验研究取得的长足进步,当然离不开理论上不断的深入。65269
在强场中高次谐波的理论研究主要分为两个方面[12]:一方面是从单原子在强激光场中响应的微观模型入手,主要研究其中高次谐波产生机制,解释高次谐波波谱的形成机理;另一方面是高次谐波产生的传播效应研究,即高次谐波在气体介质中产生后,将在宏观介质中传播一段距离,在此过程中谐波会受到气体及部分等离子体的影响,如吸收、相位匹配等。研究传播效应能够使得理论分析更加贴近实验结果。
高次谐波的辐射谱,具有明显特征的平台区和截止区(参见图1.2)。在平台区内,谐波强度随级次增加基本保持不变,而到了截止区,谐波强度迅速下降,辐射谱呈现特有的平台区以及平台区谐波规律地等频率间隔分布,这个独特的优点使得高次谐波成为产生阿秒激光的首选光源[37]。但是由于在相互作用区域,驱动激光的强度已经可以与原子内部库伦场的强度比拟,传统微扰理论的前提被打破,已经不再适用,从而无法解释这段平台区的出现[37]。新的理论普遍认可,高次谐波的产生是在隧穿电离中的一种现象。
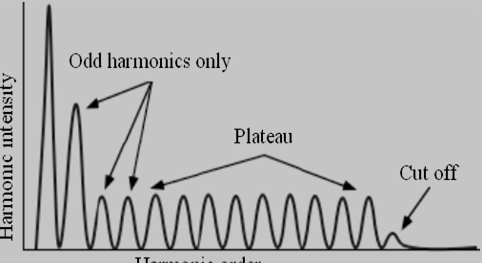
图1.2 典型的谐波谱
目前对高次谐波产生的解释通常采用P. B. Corkum提出的半经典三步模型[13]:这个模型给出,电子电离时刻驱动激光的瞬时相位决定了电子在与母核复合时所获得的动能(有质动能),从而也就决定了辐射出的谐波能量。
在高次谐波的研究过程中,涉及到微观单原子响应模型,理论上普遍使用的方法是由M. Lewenstein等人提出的一个改进了的量子理论模型[4,14],即强场近似模型(Strong-Field Approximation,简称SFA):电子波函数会从基态通过偶极跃迁占据自由态,处在自由态的电子波函数在外场的作用下会与电子的基态波函数相互干涉,干涉导致的电子偶极动量的快速振荡,将会产生电磁辐射,最终释放出来的高能光子即是所谓的高次谐波。这种量子模型在描述高次谐波产生上与半经典描述是等效的。基于量子力学的理论方法还有由K. C. Kulander和J. J. Krause提出来的单电子近似模型(Single Active Electron Approximation,简称SAE)[15,16],即仅考虑一个弱束缚电子在原子实有效势能场和激光场共同作用下的响应。具体计算是通过三维含时Schrödinger方程的数值求解来得到结果的,其模拟结果与实验结果符合得相当好,尤其是能够给出谐波的截止位置,但是这种全量子方法计算过于费时[12]。
研究高次谐波在宏观介质中的传播效应时,具体操作是将先前的单原子响应计算结果为源项,插入在宏观介质中的传播方程(即Maxwell方程)来求解。根据先前源项(即单原子响应辐射的高次谐波)采用模型的不同,又分别有基于SAE和SFA的传播方程。首先基于介绍SFA方法,E. Prori等人[12]提出了介质中三维传播方程,其中包括等离子体对基波光束的影响。之后,由N. H. Shon等人提出基于SAE方法的三维传播方程。另外根据假设条件选取的不同,又分为两类研究:绝热近似和非绝热方法[12]。绝热近似,即假设原子响应取决于激光瞬时的强度;故而非绝热是指在计算中需要考虑原子对脉冲激光场持续时间内的全部响应。最先应用于计算的是采用绝热近似的方法,但在实验上观察到现象与理论计算存在冲突,于是有必要引入非绝热方法。P. Salières等人[17]首次完全地采用非绝热方法,通过单原子响应和谐波场的三维传播来研究。论文网